historiedelosteselados

caracteristicas de los teselados

Teselados regulares

Artículo principal: Teselado regular

Los únicos polígonos regulares que cubren completamente una superficie plana son: triángulos equiláteros, cuadrados y hexágonos regulares.
En cada vértice la suma de ángulos es de 360º, para que no queden espacios:

Triángulos equiláteros
Cuadrados
Hexágonos

Ejemplo: Los cuadrados, al tener ángulos de 90°, pueden encajar cuatro por vértice y teselar localmente el entorno de dicho vértice.

Teselados semirregulares

Son aquellos que contienen dos o más polígonos regulares en su formación.
Un teselado semirregular tiene las siguientes propiedades:

Está formado sólo por polígonos regulares.
El arreglo de polígonos es idéntico en cada vértice.
Sólo existen ocho teselados semirregulares.

4 8 8
3 3 3 4 4
3 3 4 3 4
3 3 3 3 6
3 12 12
3 4 6 4
3 6 3 6
4 6 12

Teselados con figuras semi-regulares

4 8 8
3 3 4 3 4
3 3 3 3 6
3 12 12
3 4 6 4
3 6 3 6
4 6 12

Teselados irregulares

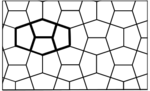
Son aquellos formados por polígonos no regulares, pero nunca dejan espacios o fisuras.

Cuadriláteros

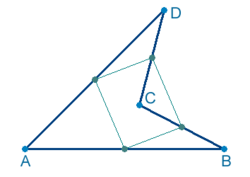
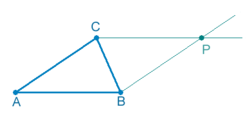
Cualquier paralelogramo tesela, ya que solo deben prolongarse sus lados paralelos y construirse los nuevos paralelogramos congruentes al primero.
Con cualquier cuadrilátero, ya sea cóncavo o convexo, es posible cubrir una superficie plana. En el caso cóncavo es fácil de demostrar, con el teorema de Varignon, que los puntos medios de todo cuadrilátero forman un paralelogramo y luego tesela. Este método se llama método de la malla invisible.

Triángulos

Con un triángulo escaleno es posible cubrir todo el plano. Esto se verifica formando el paralelogramo correspondiente.

Hexágonos

Además de los hexágonos regulares, los hexágonos no regulares con simetría central también teselan el plano. Otros hexágonos no regulares no teselan el plano.

Teselado de El Cairo

Teselado de El Cairo, Egipto.

Este teselado aparece frecuentemente en las calles de El Cairo, Egipto, y en el arte islámico; de ahí su nombre. Este pentágono posee dos ángulos rectos, un ángulo de 144° y dos ángulos de 108°. Al igual que para todo pentágono, la suma de sus ángulos es de 540°.